Modeling

These last few days have been kind of interesting, I've ditched my experiments for the time being and working on some assignments for my classes. More like final assignments that I've to turn in. Recently, over the last few months, I've been finding myself modeling a few differential equations here and there. Did you know that you can model 1D differential equations in Excel? It's kind of cute but that's what I did for my controls classes, which are all about differential equations. I kind of felt bad for my labmates that used things like Mathematica to solve these equations. I was done in about 5 minutes. I also did it once for my 4th year math 400 class.

I've gotten back into modelling for my numerical analysis course. The professor told us to go model something using differential equations and I decided to model the concentration of an electric field around a sharp point. If you ever applied a strong voltage to a needle, it will either emit a plasma or an electron beam (if it is in a vacuum).

Turns out that my project is to make an electron beam using these things called carbon nano tubes. Suffice to say, they have incredibly small diameters, on the order of several nanometers for the smallest tubes. As I have read a bunch of reserach papers in the field, I've heard all about this concentration of electric fields on carbon nanotubes and after a while it started to make sense and I decided to model it to see if my hunch was right.

For you people that studied physics out there, do you remember how to calculate the electric field inside a parallel set of plates (ie, the parallel capacitor)? Now imagine if you added a big stage in the middle of the plate. The electric field from the stage to the opposite would look like if you had the plates closer together, the electric fields from the region far away from the stage would look like it was from a set of plates with a wider gap.

Now imagine what happened if the stage got narrower and narrower and turned into a long line? What would happen is that the fields everywhere in the parallel plates will want to look a normal parallel plate capacitor leaving a strong electric field concentration at the tip of the long and slender object. You probably won't understand this just be reading this because it's the kind of thing where a drawing is necessary. Fortunately, I was up till 2 am running simulations.

The purturbed capactor potential

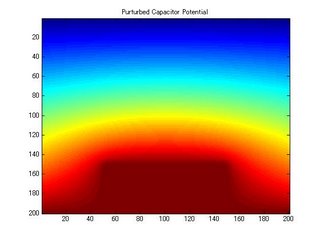
The above image is a model of a plate with a stage. The stage is in dark red and it's kept at a high voltage, the color changes represents a decreasing voltage as you move away from the high voltage region.

A figure of the the carbon nanotube potential is illustrated below.


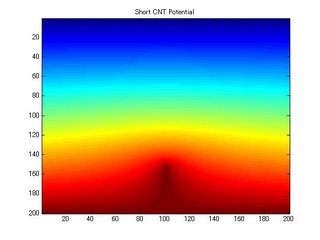
The second image, is a figure of what happens if you attach a long slender object to the plate at the bottom, for instance a Carbon nanotube. Going straight up from the tip of this object, you will notice that the color gradient changes the fastest at the tip. Regions of strong gradients in voltage represents strong electric fields, this is the property that electron emitters take advantage of when emitting electron beams.

How did I model this? There is something called Poisson's equation that can do this. The problem is that you can't find a simple function to model these equations. What Poisson's equation talks about its how things change... or how something should be distributed through a space following simple laws. Unfortunately, math books do not do a good job of explaning these ideas and most people that do figure it out, are also bad at explaining it (which explains my professors when they were teaching me differential equations).

I will have to do a better job of explaining this since I am planning on doing a seminar on numerical methods for my lab group this weekend.